Frequentist and Bayesian are two schools of thought in probability theory. Let us look at the difference between them. Bayesian and frequentist approaches are two major frameworks in statistics for analyzing data and making statistical inference.
The frequentist approach is based on the idea of probability as the long-term frequency of an event in repeated trials. In this approach, statistical inference is based on the likelihood of observing the data given a null hypothesis, assuming that the null hypothesis is true. The null hypothesis is usually a statement about the population parameter of interest, such as the mean or the proportion. The frequentist approach uses methods such as hypothesis testing and confidence intervals to assess the evidence against the null hypothesis.
On the other hand, the Bayesian approach is based on the concept of probability as a degree of belief in an event or hypothesis. In this approach, prior knowledge or beliefs about the population parameter of interest are combined with the likelihood of the data given the parameter to obtain the posterior distribution of the parameter. The posterior distribution summarizes the updated knowledge or beliefs about the parameter after observing the data. Bayesian methods use techniques such as Bayes’ theorem and Markov chain Monte Carlo (MCMC) simulation to obtain the posterior distribution.
One key difference between the two approaches is the treatment of probability. Frequentists view probability as a property of the data-generating process, while Bayesians view probability as a measure of uncertainty or belief about the parameter. Another difference is the role of prior knowledge or beliefs in Bayesian inference, which can have a strong influence on the posterior distribution.
In practice, both approaches have their strengths and weaknesses and can be applied in various settings depending on the nature of the problem and available data.
Frequentist is objective and is not influenced by personal feelings or opinions in considering and representing facts. But Bayesian is subjective, based on or influenced by personal feelings, tastes, or opinions.
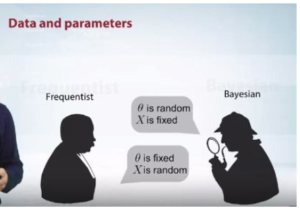
Another quick point to be noted is that in Bayesian we are willing to change our belief in light of new evidence. Here we often say in terms of probability of observing a data give parameters. Here depending upon our observation of a particular data, we choose a parameter that best explains the phenomenon.
But in frequentist, the parameters are fixed regardless of what data we observe. Another thing is the frequentist estimation gets accurate as we observe more and more data.
The differences between Bayesian and frequentist approaches in statistics can be summarized as follows:
- Probability: The key difference between the two approaches lies in their interpretation of probability. Frequentists view probability as the long-term frequency of an event in repeated trials, while Bayesians view probability as a degree of belief or uncertainty about an event or hypothesis.
- Prior knowledge: Bayesian inference explicitly incorporates prior knowledge or beliefs about the parameter of interest, whereas frequentist methods do not. The prior distribution represents the prior beliefs about the parameter, which are then updated using the likelihood function to obtain the posterior distribution.
- Hypothesis testing: Frequentist methods rely heavily on hypothesis testing, where the null hypothesis is tested against an alternative hypothesis. In contrast, Bayesian inference involves model comparison using the Bayes factor or posterior probabilities.
- Sample size: Frequentist methods tend to require larger sample sizes to obtain reliable results, while Bayesian methods can often be used with smaller samples.
- Interpretation: Frequentist methods focus on estimating the probability of observing the data given the null hypothesis, while Bayesian methods focus on estimating the posterior distribution of the parameter of interest. This allows for a more intuitive interpretation of the results in the Bayesian framework.
- Complexity: Bayesian methods are often more computationally intensive than frequentist methods, especially when using MCMC simulation to obtain the posterior distribution.
In practice, the choice between the two approaches depends on the nature of the problem, available data, and the researcher’s prior knowledge and beliefs. Bayesian methods are particularly useful when prior knowledge is available or when complex models need to be compared. Frequentist methods are often preferred when hypothesis testing is of primary interest or when the sample size is large.
Applications
Bayesian and frequentist approaches have numerous applications in statistics, including:
- Hypothesis testing: Both approaches can be used to test hypotheses about population parameters, such as the mean or proportion.
- Estimation: Both approaches can be used to estimate population parameters based on sample data, although the methods used to obtain the estimates differ.
- Model selection: Bayesian methods can be used to compare multiple models based on the evidence provided by the data, while frequentist methods can be used to compare nested models using likelihood ratio tests.
- Prediction: Bayesian methods can be used to make predictions based on the posterior distribution of the parameter of interest, while frequentist methods can be used to construct prediction intervals based on the estimated parameter.
- Decision making: Bayesian methods can be used to make decisions based on the posterior distribution of the parameter of interest, while frequentist methods can be used to make decisions based on the results of hypothesis tests or confidence intervals.
- Bayesian networks: Bayesian networks are graphical models that can be used to represent complex relationships between variables and can be used for prediction, decision making, and modeling.
- Machine learning: Bayesian methods can be used in machine learning for tasks such as classification, regression, and clustering.
- Survival analysis: Both approaches can be used for survival analysis, which involves modeling the time until an event of interest occurs.
In general, Bayesian methods are more flexible and can handle more complex models and prior information, while frequentist methods are more straightforward and easier to implement in many cases. The choice between the two approaches depends on the specific problem and available data.