The two or three-dimensional mapping of crystals in reciprocal space is known as reciprocal space mapping (RSM). The RSM is performed by a coupled scan of $2\theta-\omega$ for a set of $\omega$ values.
These maps, centered around reciprocal lattice spots, offer insights beyond those obtained from single line scans, such as high-resolution rocking curves.
In epitaxial thin films, lattice strain relaxation often induces tilting on individual layers and which in turn may results in peak displacement.
Asymmetric strain-induced displacement is evident in rocking curves. Traditional rocking curve measurements show peak broadening and overlap due to mismatch and threading dislocations.
Reciprocal space mapping (RSM) separates these effects, allowing precise measurement of Bragg peak positions. This capability is crucial for determining strain, lattice relaxation, composition, and layer thickness in multilayer thin films.
Step by Step Procedure of Reciprocal Space Mapping
The following section discusses the steps in RSM. The title figure should be referred to understand the scanning angles.
Symmetric X-ray $ω$ Scan
In $\omega$ scan, the detector is fixed at a particular angle 2$\theta$ , and the X-ray source is scanned around the Bragg peak in the range around $\pm\theta_1$ , where $\theta_1< \theta$.
The resulting rocking curve serves as a significant indicator of the material’s crystalline quality. The Full Width at Half Maximum (FWHM) of the recorded rocking curve offers information about the degree of coherency and texture of the thin film. Films of good quality exhibit FWHM < 2 $^{\circ}$.
Asymmetric X-ray $φ$ Scan
The $φ$ scan provides information about the crystal symmetry and epitaxial relationship between the film and substrate. The detector is fixed at a calculated Bragg’s angle of the particular crystal plane, and the sample has to be rotated around 360 $^{\circ}$ normal to the surface plane of the film.
Asymmetric $\theta-2\theta$ Scan
During an asymmetric $\theta-2\theta$ scan in reciprocal space mapping, X-ray radiation exposes a family of parallel planes of a thin film, oriented at an angle $χ$ to the film surface. The sample tilts by an angle $χ$ with respect to the horizontal axis to expose the desired planes for RSM analysis.
To probe the rotational symmetry along the asymmetric planes of the thin films, users rotate the sample around the perpendicular angle while keeping the source and detector fixed. They also fix the $χ$ value for a specific set of planes to be scanned.
Finally, in asymmetric mode, they fix the $φ$ and $χ$ values to perform the $\theta-2\theta$scan for the required set of planes. Since the asymmetric planes align at a certain angle with the in-plane crystallographic axes, researchers typically use the asymmetric XRD pattern to evaluate the in-plane lattice parameters of the crystal.
Calculation of Lattice Parameter using Reciprocal Space Mapping
The RSM is carried out by changing $ω$ for a constant step size (Δω) while maintaining the range of $2\theta$ fixed.
The component of the scattering vector parallel to the crystal plane is expressed as:
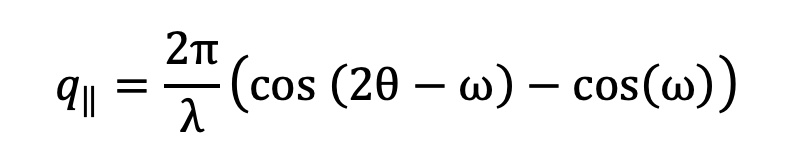
The in-plane lattice parameter can be calculated using the expression:

End note
I personally found this video incredibly helpful in enhancing my understanding of reciprocal space mapping techniques. It offered visual clarity that enriched my knowledge on the topic.
We aim to offer informative and engaging content, and your comments aid us in tailoring our articles to better match your interests and needs.
Please don’t hesitate to share your thoughts, questions, or suggestions in the comments section below the video. We eagerly anticipate hearing from you!
