An activation function in deep learning is a nonlinear transformation applied to the node output before passing it to the consequent layers in neural networks.
Artificial Neural Networks (ANN) consist of multiple layers interconnected. Mainly there will be an input layer, output layer and one or more hidden layers. Inspired by the biological neural networks, ANNs have nodes which mimics neurons in human brain.
The input layer receives raw data to be processed and pass it to the hidden layers to process it. After the initial processing, the data will be passed to the output layer for classification or regression tasks. As demonstrated in the title schematic, each neuron creates a weighted sum of its inputs as a scalar quantity and passes it to a function called activation function. Activation functions are also called transfer functions as it helps to enable the process of result extraction at the output of a node.
Significance of Activation Functions in Neural Networks
Activation functions helps to map the output of a neural network within a range like $(0,1)$ or $(-1, +1)$. For instance, if the trend or characteristic of the output is like linear function extending from $-\infty$ to $+\infty$, nonlinear activation function can be used to confine it in a finite range. The output transferred to finite range are easy to understand and interpret.
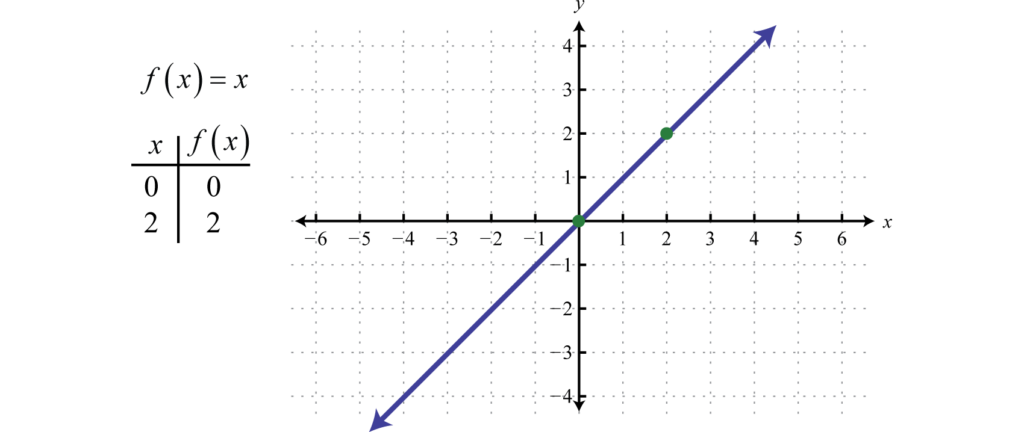
Figure 1. Output behaviour without activation function (source: saylordotorg.github.io)
The essential characteristics of activation functions are as follows:
- The activation functions should be differentiable. This means we should be able to track the change in $y$-axis (vertical axis) of an activation function in response to the $x$-axis (horizontal axis). The ratio of change in $y$-axis to the change in $x$-axis between any two distinct points on a line is called slope.
- The activation functions should be monotonic. The monotonic functions will either increase or decrease in the entire range of consideration.
The following part of this article gives a glimpse of commonly used activation functions in neural networks.
Sigmoid
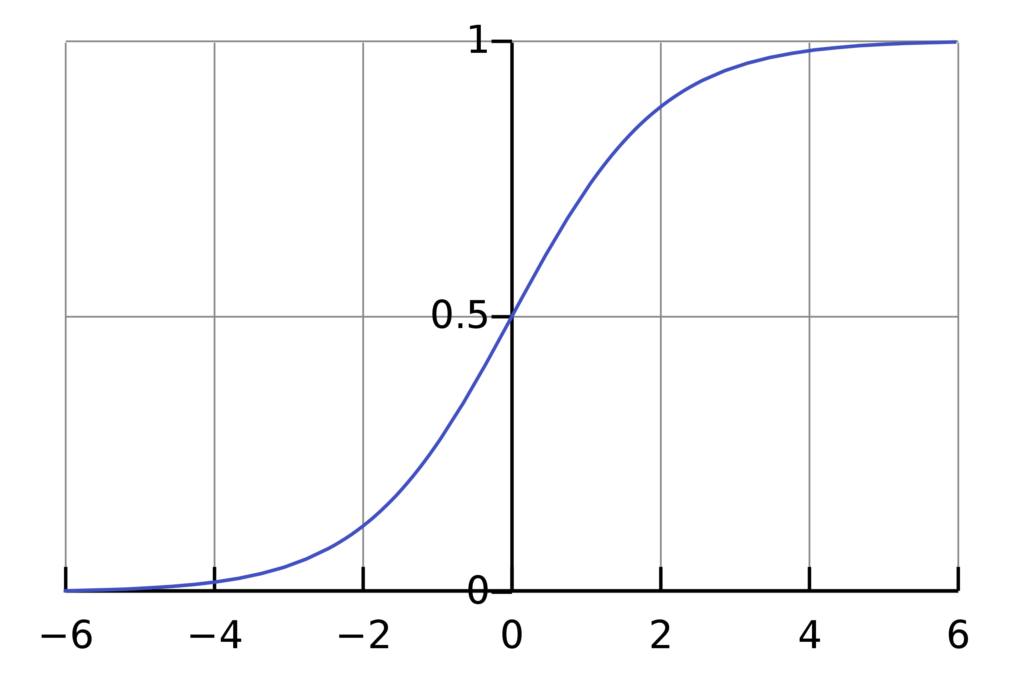
Figure 2. Sigmoid activation function (source: Wikipedia)
The sigmoid function confine to the range of 0 to 1. The probability of any outcome also belongs to the range of 0 to 1. Hence, sigmoid function serves as a suitable choice of activation function in models which are meant to predict probability.
The sigmoid function is also called logistic activation function as it is used in logistic regression for binary classification. Softmax function is more generalized version of the logistic activation function used for multiclass classification.
The softmax function is differentiable as well as monotonic in nature. However, the derivative of this function is not monotonic. The sigmoid function output is not zero-centered and often encounter vanishing gradient problem. This increases the model complexity.
Rectified Linear Unit (ReLU)
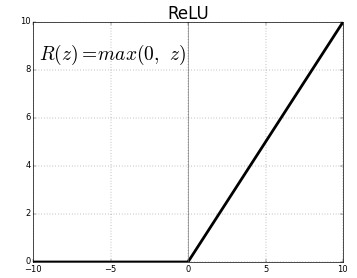
Figure 3. ReLU activation function (source: Analytics Vidhya)
As the name suggests, ReLU follows a partially rectified pattern as demonstrated in Fig.3. ReLU is nowadays a favorite choice of activation function in most convolutional neural networks. The range of ReLU is 0 to infinity. The function as well as its derivative is monotonic in its characteristic behaviour.
ReLU fails to fit the entire data if it is a mix of positive as well as negative values. As rightly demonstrated in Fig.3. , $R(z)$ is zero for $z$ values less than zero. This implies ReLU converts the negative input values to zero which in turn results in inappropriate mapping of negative data points. This situation is called the dying ReLU problem. Leaky ReLU is an activation function with slight modification to ReLU to overcome the dying ReLU problem.

Figure 4. Leaky ReLU activation function (source: Papers With Code)
The range of leaky ReLU function is from $-\infty$ to $+\infty$. As evident in Figure 4., while using the leaky ReLU function, the function $f(y)$ will not dye out for negative input values of $y$.
The typical value of the coefficient “$a$” is 0.01. In some problems, $a$ is assigned with random values different from the value 0.01. Such ReLU functions with randomly assigned “$a$” values are called Randomized ReLU. ReLU functions and its derivatives in general are monotonic.
Hyperbolic tangent (Tanh)
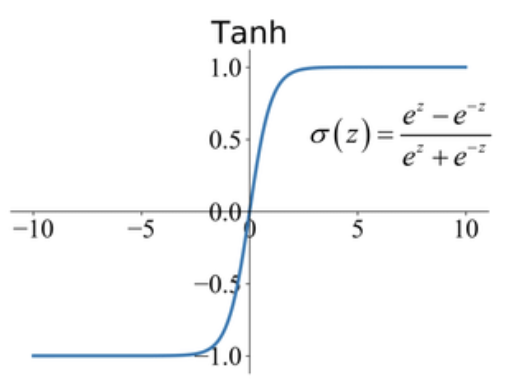
Figure 5. Tanh activation function (source: Papers With Code)
Tanh is an activation function with S-shaped response as in the figure in the range $-1$ to $+1$. It is mainly used for classification purposes. The Tanh activation function maps the zero input values to nearly zero values and the negative values in input data to strongly negative values.
The Tanh function is monotonic in response and differentiable. However, the derivative of the Tanh function is not monotonic. The Tanh function is more similar to the sigmoid function and hence this function is computationally expensive.
End note
Although there are no hard and fast rules to select an activation function for a particular problem, the following remarks could be helpful to make the right choice of activation function.
- ReLU is an activation function that can be suitable in most cases. Leaky ReLU and randomized ReLU can rescue in cases where we encounter dead neuron problems.
- Sigmoid function or Tanh function or the combination of both functions can be a suitable choice for classification tasks. However, precautions should be taken to tackle the vanishing gradient problem.
- ReLU can be tried as a first choice in most of the tasks. In cases where further better optimization of output is required, other activation functions and their combinations can be tried.
