Density Functional Theory (DFT) stands as a cornerstone in the realm of quantum mechanics, serving as a powerful tool for understanding the electronic structure and properties of materials. In this article, we will embark on a journey to demystify DFT, exploring its fundamental principles, applications in material science and physics, and the practical aspects of running DFT simulations.
Unlike traditional quantum mechanical approaches that focus on individual electron wave functions, DFT zooms in on electron density – a key factor that governs the behavior of matter at the quantum level.
For more basic aspects, go through the article “A Lighter Perspective to Density Functional Theory“
Principles of Density Functional Theory
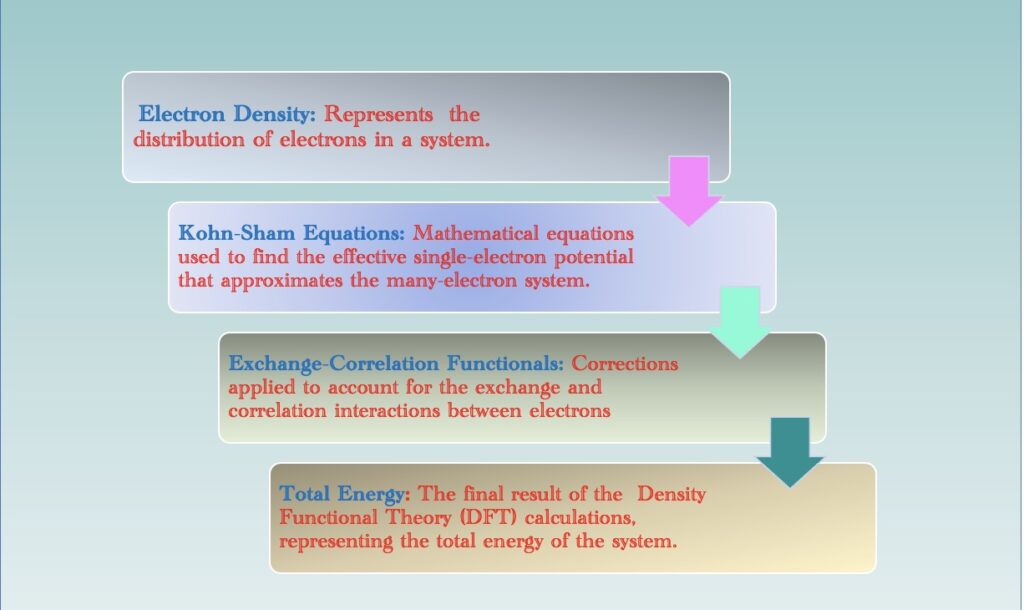
DFT operates on a set of fundamental principles that form the bedrock of its computational approach to studying the electronic structure of materials. At its core, DFT revolves around the Kohn-Sham equations, which provide a practical and efficient means to address the many-body problem in quantum mechanics.
These equations introduce the concept of an effective single-electron potential, allowing researchers to approximate the complex interactions within a many-electron system. Consequently, DFT shifts the focus from dealing directly with individual electron wavefunctions to a more tractable and insightful consideration of electron density.
Kohn-Sham Equations
The Kohn-Sham equations are a set of mathematical equations used in Density Functional Theory (DFT) to describe the electronic structure of a many-electron system. The central idea is to map the interacting many-electron system to a non-interacting system with an effective potential. The Kohn-Sham equations consist of two key components: the kinetic energy operator $T_s$ and the effective potential $V_{\text{eff}}$. The general form of the Kohn-Sham equation for a single electron in an external potential $V_{\text{ext}}$ is given by:
$$\hat{H}_{\text{KS}}\psi_i(\mathbf{r}) = \epsilon_i\psi_i(\mathbf{r})$$
Where:
- $\hat{H}_{s\text{KS}}$ is the Kohn-Sham Hamiltonian.
- $\psi_i(\mathbf{r})$= represents the Kohn-Sham orbital for the (i)-th electron.
- $\epsilon_i$ is the energy eigenvalue associated with the (i)-th orbital.
The Kohn-Sham Hamiltonian $\hat{H}_{\text{KS}}$ consists of the kinetic energy operator $T_s$, the external potential $V{\text{ext}}$, the electron-electron repulsion energy $V_{\text{ee}}$, and the exchange-correlation potential $V_{\text{xc}}$:
$$\hat{H}_\text{KS} = T_s+V_{ext}+V_{ee}+V_{xc}$$
In this equation:
- $T_s$ is the kinetic energy operator.
- $V_{\text{ext}}$ is the external potential, typically arising from the interaction with atomic nuclei.
- $V_{\text{ee}}$ is the electron-electron repulsion energy.
- $V_{\text{xc}}$ is the exchange-correlation potential, accounting for the effects of electron exchange and correlation.
The Kohn-Sham equations are solved iteratively, self-consistently, until a converged set of orbitals and energies is obtained, providing a realistic description of the electronic structure of the system within the DFT framework.
Exchange Correlation Functional
In practical terms, the Kohn-Sham equations are supplemented by exchange-correlation functionals, indispensable components in the DFT framework. These functionals correct for the limitations of traditional density-only calculations by accounting for the exchange and correlation interactions among electrons. This inclusion enhances the accuracy of DFT calculations, making it a versatile and reliable tool in predicting diverse material properties.
The iterative solution of the Kohn-Sham equations, facilitated by the exchange-correlation functionals, converges towards a stable electronic structure. This convergence, coupled with the self-consistent nature of DFT calculations, ensures that the resulting electron density accurately represents the equilibrium state of the system under investigation.
The principles of Density Functional Theory hinge on the pragmatic application of the Kohn-Sham equations, enhanced by exchange-correlation functionals. This methodological approach empowers researchers to gain valuable insights into the electronic structure of materials with a level of computational efficiency that has become synonymous with DFT’s widespread success in the scientific community.
Running DFT Simulations: Tools and Techniques
To harness the power of DFT, researchers often turn to sophisticated software packages, such as Quantum ESPRESSO, VASP (Vienna Ab initio Simulation Package), or GPAW. Let’s outline the steps for installing Quantum ESPRESSO, a widely-used DFT software:
- Download and Installation:
- Visit the official Quantum ESPRESSO website.
- Follow the provided instructions for downloading the software.
- Execute the installation commands specific to your operating system.
- Input Preparation:
- Construct an input file specifying the system, calculation parameters, and desired output.
- Define the crystal structure, boundary conditions, and any additional settings relevant to the simulation.
- Execution:
- Run the simulation using the prepared input file.
- Monitor the progress and check for convergence.
- Analysis:
- Examine the generated output files to extract valuable information about the system’s electronic structure and properties.
Applications of DFT in Material Science and Physics
DFT’s versatility makes it indispensable in various scientific domains. Let’s explore two key areas where DFT plays a pivotal role:
- Material Science: DFT has revolutionized materials research by predicting and understanding properties like electronic band structures, formation energies, and phonon spectra. For instance, researchers use DFT to explore novel materials for electronic devices, catalysts, and energy storage.
- Physics: In physics, DFT aids in the study of fundamental phenomena, such as the electronic properties of nanoscale structures, magnetic interactions, and phase transitions. For instance, DFT simulations can unveil the intricate details of magnetic materials’ behavior under different conditions.
Conclusion: Unleashing the Potential of Density Functional Theory
In conclusion, Density Functional Theory serves as a formidable ally in unraveling the mysteries of the quantum world. With its application spanning from material science to physics, DFT continues to drive advancements in scientific understanding and technological innovation. As researchers delve deeper into the intricacies of DFT, the possibilities for uncovering new frontiers in quantum science remain limitless.
Endnote
As we wrap up our exploration into the principles of Density Functional Theory, your insights and feedback are invaluable. Your thoughts play a pivotal role in shaping our upcoming discussions, ensuring we tailor our content to your specific interests.
Looking ahead, our upcoming articles will actively examine real-world applications of DFT in physics and material science. We’ll dissect example cases, vividly illustrating how DFT reveals the intricate details of quantum phenomena and contributes to groundbreaking discoveries in the realms of physics and materials.
Your curiosity propels us forward, and we eagerly anticipate continuing this journey through the fascinating landscapes of Density Functional Theory.