“Small parts of curves are nearly straight line“
I heard this first-time years back in one of MIT’s OpenCourseWare calculus classes. Little did I know it is going to be a life-long lesson to me at that time.
This concept is going to be one of the first principles we will be dealing with in many situations. I have encountered it in so many places and applications.
In that particular class the professor was explaining derivatives and how we can compute derivatives are ratios. He was telling about how we get the expression for derivative. The secant becomes the tangent. The ratio of change in output variable with respect to the input variable gives us another algebraic expression. This tells us the derivative value at every point.
The following figure shows this concept graphically.
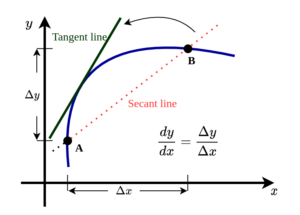
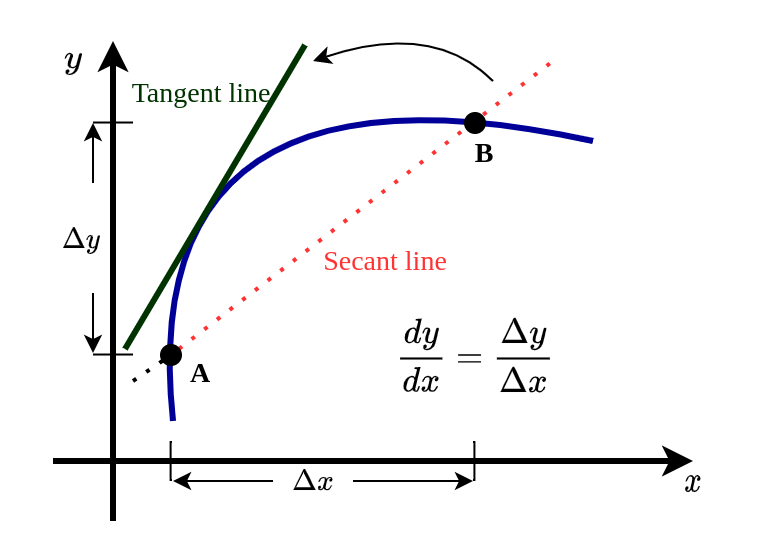
Here the blue curve is our function or graph of interest. Please note that it is not like the graphs start at some point and stop somewhere. It might be one continuing to both sides of the x-axis. But for the explanation purpose, we only focus on a part of it.
The question here is how does the graph change as x-values change? or what is the rate of change?. The answer to this can be found using a simple ratio of the change to y-values to change in x-values.
Since the graph is not a straight line, we might get different ratios for different $\Delta x $ values. Infact $\Delta$ means only a small change.
As we reduce $\Delta x$ to smaller values, the secant line becomes the tangent line and we get the derivative for the function at the point the tangent touches the graph.
You might be thinking, as we go for smaller and smaller $\Delta x$ values, Isn’t it $\Delta x$ becomes zero?. Also won’t that make $\Delta y $ zero?. This is where the concept of limit comes.
The short answer is NO. Neither $\Delta x$ or $\Delta y$ goes zero. It just approaches pretty closer to zero. The more important thing is the ratio of $\frac{\Delta x}{\Delta y}$ start to converge to a particular value as $\Delta x$ approaches zero.
For me, the concept of limit was not at all obvious. Though it may not seem very complicated, there is a high chance of us missing the intuition here. The concept is so fundamental building block but often goes unnoticed or underrated.
Now coming back to our core idea. Even though the graphs we consider are wiggly or curvy, we were able to concentrate on a tiny region of it. And along with it the convergence property helped us figure out the derivative value at that point.
Did you missed the crux idea here?.
Yes, for me the key idea here is that we were able to concentrate on a tiny part of a big problem, so tiny that even though the problem as a whole was challenging, the tiny part was easy for us to solve and move to the next tiny part. In this way, we were able to solve the whole problem.
In real-life
Now let’s see some real-life situations where this idea comes in.
Many times I have read from people going through tough military training is that they get through things just by focusing on the moment.
IF we think of a task as a whole, we will be scared to do anything. When you are not feeling like working/exercising/studying you can always try to divide the task into a tiny thing, accomplish that, and then get going.
Another scenario might be our perception of the earth being flat. Humans’ physical dimension is so small compared to the earth’s size so that it looks flat to us. Just like when we looked at a tiny region of $\Delta x$, it appeared straight to us. Once it was straight, it became much more manageable.
Example from Trignometry
Let us look at another example that is rooted on the idea. You might have learned this trig identity in your school/college days.
$\lim_{\theta\to 0} \frac{sin(\theta)}{\theta} = 1$,
We can try to understand it graphically and algebraically.
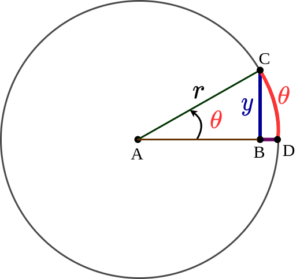
As we can see here it is a unit circle and hence the radius $r$ =1.
A right-angled triangle $\angle ABC$ is drawn inside the unit circle. The hypotenuse $AC$ and line segment $AD$ has the same unit length. An angle $\theta$ ($\angle CAD$) exist inside.
For right-angled triangles, we know the relation,
$sin(\theta) = \frac{\text{opposite side}}{\text{hypotenuse}}$,
Here we have line segment $BC$ as opposite side and hypotenuse ($r$) is 1. Hence $sin(\theta)$ becomes the same as length of line segment $BC$ itself.
Now let’s see what will happen if we let the $\theta$ go to a smaller and smaller value. We can see the length of $BC$ and $CD$ are somewhat closer. Since $CD$ is curved, it is expected to be a bit lengthier than $BC$.
As $\theta$ goes infinitely small, the difference becomes negligible and they both approach of same length and their ratio becomes 1 also.
Again we saw when we zoom in, how small parts of curves are becoming straight lines.
The transformation from curve to straight line made the length and ratio calculation easier. In life also, we get to get through things much easier when we focus only on a tiny part of it.
Algebraic Intuition
Now let’s see this unit circle intuition algebraically.
You might now the algebraic Taylor series expression for $sin(\theta)$.
$\sin(\theta) = \theta – \frac{\theta^3}{3!}+\frac{\theta^5}{5!}-…$
Imagine what will be happening when $\theta$ approach to zero.?
All the terms except the first one die out too quickly as we are taking powers of fractions ($\theta^k$). If you think of it in the form of a polynomial regression (where the coefficients are the inverse factorial terms), you can imagine as $\theta$ approaches zero, the curvy red region becoming a straight line or same as $BC$.
Conclusion
We have seen the concept from at least three perspectives. It keeps appearing in science and engineering over and over again. It is a keystone to calculus, used with approximating functions, or sometimes as a building block to another concept. We will revisit it in our journey of understanding other concepts at later points.