A Markov Decision Process (MDP) is a mathematical framework used to model decision-making situations where the outcome of a decision depends on both the current state of the system and the actions taken by the decision maker.
In an MDP, the decision maker is represented as an agent, and the system is represented as a set of states that the agent can transition between based on the actions it takes. Each state has a certain reward associated with it, which the agent aims to maximize over time. The agent’s actions affect the state transitions and the rewards obtained, and the goal is to find the optimal policy, or sequence of actions, that maximizes the long-term reward.
The key assumption in an MDP is the Markov property, which states that the probability of transitioning from one state to another only depends on the current state and action taken, and not on any past history. This means that the future state and reward are independent of the past, given the current state and action.
MDPs are commonly used in many fields, including engineering, economics, and computer science, to model decision-making problems such as robot navigation, financial portfolio management, and game theory. They are often solved using dynamic programming algorithms, which involve iteratively updating the value function, or expected long-term reward, for each state based on the current policy. Other methods, such as Monte Carlo simulation and reinforcement learning, can also be used to solve MDPs.
Intuition behind Markov Decision Process
The intuition behind a Markov Decision Process (MDP) can be illustrated using a simple example of a robot trying to navigate a room.
In this example, the robot is represented as an agent, and the room is represented as a set of states. Each state represents the robot’s location in the room, and the robot can take different actions to move to another state. For example, the robot can move forward, turn left or right, or stop.
Each state has a certain reward associated with it, which represents how good or bad that state is for the robot. For instance, a state close to the exit might have a high reward, while a state with obstacles or a long distance from the exit might have a low reward.
The goal of the robot is to find the optimal policy, or sequence of actions, that maximizes the long-term reward. To achieve this, the robot needs to take into account not only the current state but also the future states that it might transition to and the rewards associated with them.
The Markov property comes into play here, which means that the probability of transitioning to a future state depends only on the current state and action, and not on any past history. This allows the robot to make decisions based on its current state and expected future states, without needing to consider the entire history of states it has been through.
MDPs provide a mathematical framework to model decision-making problems like this and find the optimal policy that maximizes the long-term reward. This involves iteratively updating the value function for each state based on the current policy, and then updating the policy based on the new value function.
Overall, MDPs provide a powerful tool to model and solve decision-making problems in various fields, including robotics, economics, and game theory.
A toy example
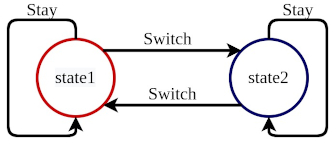
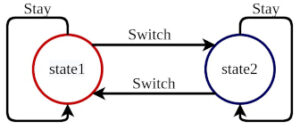
This is an example on how to implement a two-state Markov Decision Process (MDP). It has only two states: state 1 and state 2. Applications MDPs often appear in machine learning and reinforcement learning.
At any stage, the agent can take any of the two actions. The actions are to stay or switch. The switch will change the current state to the other one and stay won’t make any changes.
At any point in time, we can print out the current state of the system. The state transition diagram can be visualized as below.
The following code implements the MDP and its fuctionalities.
class TwoStateMDP(object):
"""docstring for TwoState"""
def __init__(self):
self.states = 2
self.nactions = 2
self.currentS = 1
def stay(self):
pass
def toggle(self):
if self.currentS ==1:
self.currentS=2
else:
self.currentS=1
switch = TwoStateMDP()
print(switch.currentS)
switch.toggle()
print(switch.currentS)
switch.toggle()
print(switch.currentS)
As you can see coding it in the form of class can make the implementation easy. We could define the states of MDP, current states, actions possible, etc.
Separate functions have been written to do the possible actions ‘stay’ and ‘toggle’.
While running the code we get the following output.
1
2
1
The command ‘switch = TwoStateMDP()’ generate an object of the two-state MDP type. By default, it will be of state 1. When we call the ‘toggle()’ function, it gets switched to the other state.
Applications of MDPs
Markov Decision Process (MDP) has a wide range of applications in various fields, including:
- Robotics: MDPs are commonly used in robotics to model the behavior of autonomous agents, such as drones or self-driving cars, and to plan their trajectories. MDPs can help robots learn optimal behaviors in complex environments and avoid obstacles.
- Finance: MDPs are used in finance to model decision-making problems, such as portfolio optimization and risk management. MDPs can help investors make optimal investment decisions based on their risk preferences and market conditions.
- Healthcare: MDPs are used in healthcare to model patient behavior and optimize treatment plans. MDPs can help doctors and clinicians determine the best course of treatment for a patient based on their medical history, symptoms, and expected outcomes.
- Game theory: MDPs are used in game theory to model strategic decision-making problems, such as in chess, poker, or other games. MDPs can help players develop optimal strategies based on the current state of the game and the possible future outcomes.
- Manufacturing: MDPs are used in manufacturing to optimize production processes and inventory management. MDPs can help factories determine the optimal level of production and inventory based on demand forecasts and supply chain conditions.
- Traffic management: MDPs are used in traffic management to optimize traffic flow and reduce congestion. MDPs can help traffic managers determine the best routing and signaling strategies based on real-time traffic data and predicted traffic patterns.
Overall, MDPs provide a powerful tool to model and solve decision-making problems in various fields and can help decision-makers make better and more informed decisions based on complex, uncertain, and dynamic environments.
Drawbacks
While Markov Decision Processes (MDPs) have many applications and benefits, there are also some limitations and drawbacks to consider:
- Computationally expensive: MDPs can be computationally expensive to solve, especially for large and complex problems. The dynamic programming algorithms used to solve MDPs require large amounts of memory and processing power, which can limit their scalability and efficiency.
- Sensitivity to model assumptions: MDPs are based on certain assumptions, such as the Markov property, which may not always hold true in real-world situations. If the assumptions are not met, the MDP model may not accurately capture the decision-making problem and may lead to suboptimal or incorrect decisions.
- Limited to discrete state and action spaces: MDPs are typically formulated for problems with discrete state and action spaces, which can limit their applicability to problems with continuous or high-dimensional spaces.
- Limited to single-agent problems: MDPs are primarily designed to model single-agent decision-making problems, which may not accurately capture multi-agent situations where multiple agents are interacting and making decisions simultaneously.
- Difficulty in modeling complex environments: MDPs may not always be able to accurately model complex environments with high levels of uncertainty and ambiguity, such as natural language processing or social interactions.
Overall, while MDPs are a powerful tool for decision-making, they are not a panacea and may not always be the best solution for every problem. It is important to carefully consider the assumptions and limitations of MDPs when using them to model decision-making problems.