Introduction
Iterative Policy Improvement (IPI) is an algorithm in reinforcement learning to find the optimal course of action given the enviroment conditions. This blog post explains how it is done using a simple grid world navigating example. It works by iteratively improving an initial policy using the policy evaluation and policy improvement steps.
Here’s how it works:
- Policy evaluation: The first step in IPI is to evaluate the current policy. This involves running the policy and collecting data on the rewards obtained. The goal is to estimate the value function of the policy, which tells us the expected cumulative reward for each state in the environment.
- Policy improvement: Once the value function has been estimated, we can use it to improve the policy. The goal is to find a new policy that is better than the current policy, by selecting actions that lead to higher expected rewards. This can be done by selecting the action that has the highest expected value according to the value function.
- Policy iteration: The new policy is then evaluated and improved in the same way as the original policy, creating a loop that iteratively improves the policy until convergence.
The key idea behind IPI is to use the value function to guide the search for better policies. By estimating the value of each state, we can determine which actions are likely to lead to the highest expected rewards, and use this information to select better policies. Over time, the policy converges to the optimal policy that maximizes the expected reward for the given task.
In this tutorial, I am going to code up the iterative policy improvement algorithm. It starts from a uniform random policy, computes the value function, and use it to update the policy again. This process continuous until the optimal policy is reached. The policy evaluation part was covered on a previous tutorial. This tutorial is an extension on that.
The grid world example and psuedo-code are taken from the University of Alberta’s Fundamentals of Reinforcement Learning course. The lecture corresponding to this tutorial can be found here. Please note that my implementation has a slight variation in the value function. This because of the way I coded up the environment.
The Grid World
Iterative Policy Evaluation
Optimal Value Function and Policy
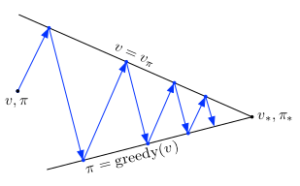
The policy is updated with value function and wiseversa. This is continued until optimal policy is reached. i.e. policy $P_{n+1}$ becomes same as policy $P_n$. The following figure shows this conceptual process of iterative policy and value function improvement.
Code
The code to reproduce the results are given below.
#!/usr/bin/python
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
class Env(object):
def __init__(self):
# self.states = np.zeros((4,4))
self.states = np.random.random((4, 4))
# self.fstates = np.zeros((4,4))
self.fstates = np.random.random((4, 4))
class Agent(object):
def __init__(self, start=[0, 0]):
self.start = start
self.cstate = start
self.reward = 0.
self.validActions = ['U', 'D', 'L', 'R']
self.policy = np.ones((4, 4, 4))
# self.policy = np.random.randint(0, 2, size=(4,4,4))
self.npolicy = np.zeros((4, 4, 4))
def showPolicy(
self,
E,
k=0,
m='',
):
arrows = '\xe2\x86\x91\xe2\x86\x93\xe2\x86\x90\xe2\x86\x92'
shift = np.array([(-0.4, 0.), (0.4, 0.), (0., -0.4), (0., 0.4)])
(fig, ax) = plt.subplots()
for ((i, j), z) in np.ndenumerate(E):
ax.text(j, i, round(z, 4), ha='center', va='center')
for action in self.validActions:
ai = self.validActions.index(action)
dirs = self.npolicy[:, :, ai] > 0
self.npolicy[:, :, ai] = dirs
for ((i, j), f) in np.ndenumerate(dirs):
if f:
ax.text(j + shift[ai][1], i + shift[ai][0],
arrows[ai], ha='center', va='center')
ax.text(self.cstate[1] - 0.25, self.cstate[0], ':-)',
ha='center', va='center')
ax.matshow(E, cmap='winter')
plt.title(m)
plt.axis('off')
# plt.show()
plt.savefig('Junkyard/anim' + str('{0:0=4d}'.format(k)) + '.png'
, dpi=80)
plt.close()
def checkNextState(self, action):
if action not in self.validActions:
print 'Not a valid action'
elif action == 'U':
nstate = [self.cstate[0] - 1, self.cstate[1]]
self.reward = -1.
elif action == 'D':
nstate = [self.cstate[0] + 1, self.cstate[1]]
self.reward = -1.
elif action == 'L':
nstate = [self.cstate[0], self.cstate[1] - 1]
self.reward = -1.
elif action == 'R':
nstate = [self.cstate[0], self.cstate[1] + 1]
self.reward = -1.
if nstate[0] < 0 or nstate[0] > 3 or nstate[1] < 0 or nstate[1] \
> 3:
self.reward = -1.
nstate = self.cstate
if nstate == [0, 0]:
self.reward = 0.
if nstate == [3, 3]:
self.reward = 0.
return nstate
def takeAction(self, action):
self.cstate = self.checkNextState(action)
def gpolicy(self, state, a):
a = ['U', 'D', 'L', 'R'].index(a)
return self.policy[state[0], state[1], a]
def policyEvaluation(myEnv, myAgent, commands):
k = 0
while True:
k += 1
for ((i, j), z) in np.ndenumerate(myEnv.states):
sums = 0
myAgent.start = [i, j]
myAgent.cstate = [i, j]
for act in commands:
if myAgent.start == [0, 0]:
step = [0, 0]
myAgent.reward = 0.
break
elif myAgent.start == [3, 3]:
step = [3, 3]
myAgent.reward = 0.
break
else:
step = myAgent.checkNextState(act)
sums += 0.25 * (myAgent.reward + myEnv.states[step[0],
step[1]])
myEnv.fstates[i, j] = sums
m = 'Performaing Policy Evaluation-Iteration ' + str(k)
# myAgent.showPolicy(myEnv.fstates,k,m)
myEnv.states = myEnv.fstates
if k > 200:
break
def policyImprovement(myEnv, myAgent, commands):
k = 0
for ((i, j), z) in np.ndenumerate(myEnv.states):
k += 1
myAgent.start = [i, j]
myAgent.cstate = [i, j]
oldacts = myAgent.policy[i, j, :] > 0
nextas = []
for act in commands:
if myAgent.start == [0, 0]:
step = [0, 0]
myAgent.reward = 0.
break
elif myAgent.start == [3, 3]:
step = [3, 3]
myAgent.reward = 0.
break
else:
step = myAgent.checkNextState(act)
nextv = myAgent.reward + myEnv.states[step[0], step[1]]
nextas.append(nextv)
if len(nextas):
newdir = nextas == np.max(nextas)
olddir = myAgent.policy[i, j, :] == 1.
if sum(olddir != newdir) > 0:
# print('Found Change at: ', i, j)
myAgent.npolicy[i, j, :] = newdir
# m = 'Performaing Policy Improvement at Cell ('+str(i)+','+str(j)+')'
# myAgent.showPolicy(myEnv.fstates,k,m)
policyStable = False
myEnv = Env()
myAgent = Agent([0, 0])
commands = ['U', 'D', 'L', 'R']
while ~policyStable:
policyEvaluation(myEnv, myAgent, commands)
policyImprovement(myEnv, myAgent, commands)
policyStable = (myAgent.policy == myAgent.npolicy).all()
if ~policyStable:
myAgent.policy = myAgent.npolicy
if policyStable:
m = 'Found Optimum Policy & Value Function'
print m
# k = 0
# myAgent.showPolicy(myEnv.fstates,k, m)
myAgent.cstate = np.random.randint(0, 4, size=(1, 2))[0]
# myAgent.cstate = np.array((1,2))
k = 0
while True:
myAgent.showPolicy(myEnv.fstates, k, m='Navigating')
k += 1
a = myAgent.policy[myAgent.cstate[0], myAgent.cstate[1]]
bacti = np.where(a == 1)[0]
if bacti.shape[0] > 1:
myAgent.showPolicy(myEnv.fstates, k, m='Breaking Ties')
k += 1
bacti = np.random.choice(bacti)
else:
bacti = bacti[0]
myAgent.showPolicy(myEnv.fstates, k, m='Taking ' + commands[bacti])
k += 1
myAgent.takeAction(commands[bacti])
if myAgent.cstate == [0] * 2 or myAgent.cstate == [3] * 2:
myAgent.showPolicy(myEnv.fstates, k, m='Reached.... :-)')
k += 1
break
