Throughout my academics when I come across the term tensor, my brain send reflex that “something complicated, take a break, relax and read later”. Often, I gave a thought, Am I reading it Tensor or Terror!! Physicists use Tensors to describe properties of systems which vary with direction called anisotropic systems whereas for mathematicians Tensors are algebraic objects to demonstrate multilinear relations in vector space. So, if we are not a physicist with special focus on anisotropic systems or not a mathematician with curiosity on interrelations of numbers at higher dimensions, whether it is wise to spend time on understanding this concept “Tensor”. We all are in real life where perceptions change when we look at a matter in different angle. So sooner or later there will be occasions where you will need to use Tensors to figure out the outcome of your perceptions in real life. This concept can help you interpret it easier. Yeah, this is an attempt to express a concept in simple way which appears complicated.
Considering cause-effect relationships in Homogeneous isotropic systems, the effect and the cause of the effect will be in same direction. So, it requires a single number to relate the effect to cause for example if we applied a force on a piece of glass, the glass will move along the direction of applied force. So, a scalar number is sufficient to describe the response of glass to the applied force. Hence there is no need of a directional indicator (basis vector) to understand this and so this is a Tensor of rank zero situation.
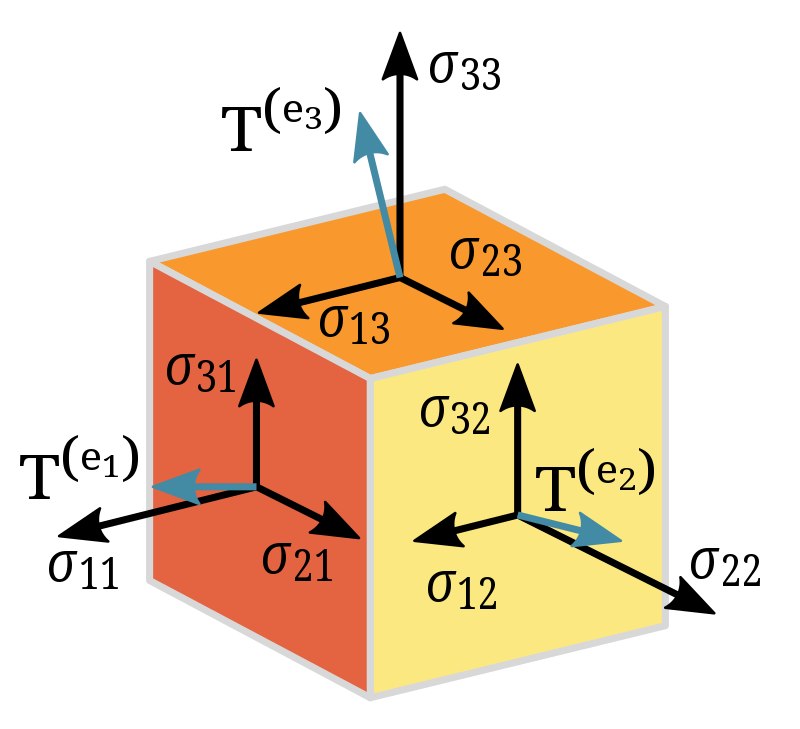
But, when dealing with cause-effect of inhomogeneous anisotropic systems, direction plays an important role in the relationship. Irrespective of the cause is a scalar or vector quantity, we need to describe the effect in multiple directions as it can be different in different directions. Suppose , A set of coordinates such as $(x, y, z)$ is used to describe the effect and can express in terms of a vector $\vec{A}{}= x\hat{i}+y\hat{j}+z\hat{k}$ , this vector will give a single magnitude as $\sqrt{x^2+y^2+z^2}$ i.e. if $(x, y, z)= (0,0,2)$ ,the magnitude is 2. The components of this vector change for anisotropic systems when we measure it with respect to a different direction and it give a different value for the magnitude. Hence it is necessary to develop some predictability on the behavior of such systems when coordinate change. Tensor was designed with some coordination transformation rules on vectors which can ensure the probable behavior of the system with direction.
For those who still don’t feel the concept is simple, take a cubical chewing gum and squeeze it along $x$-direction , the chewing gum will contract along the $x$-direction and elongate along the other two directions ($y$ and $z$ ). So it is easy to express the behavior of chewing gum by assuming it linear. And if we are clear about this by giving the input along $x$, $y$ or $z$ direction , we can understand the behavior along the oblique directions also by resolving it into components (multi linear) and adding the components along each direction to ensure the complete description and this step is mathematically expressed in terms of tensor .
To concise, Tensor allows the transformation such a way to get the same result irrespective of the reference frame from which we are taking measurement. When the direction of observation (basis vector) change, the change in coordinates will be such a way to keep the combination of coordinates and basis vector are same for all observers. Hence Lillian Lieber called Tensors as the facts of the universe.