Bellman operators come in Reinforcement Learning (RL). When I first encountered it, I had many questions regarding it. I often feel it is interesting to observe that what feels intriguing to someone. Many questions surface out in our minds.
Why is it called an operator?. What are the inputs to it and output from it?. What properties does it hold?. Who is Bellman anyway?. Regarding Bellman operator, I spent some time answering such questions. This blog post is a documented version of the answers I found.
The Mathematical Operator
From the mathematical point of view, an operator is a mathematical object that does some transformation to its input.
A simple example could be $y=x+1$, in this mathematical expression whatever be the quantity in $x$ will be incremented by 1 and will be represented by the variable $y$. The ‘$+$’ here is a mathematical operator.
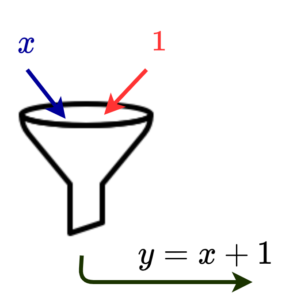
Wikipedia defines a mathematical operator as a function or mapping that acts on elements in one space and produce elements of another space or even the same space. Here the space in this example is a set of real numbers. Adding 1 to them maps them to the same space itself.
It is through one or more combinations of such operators we describe transformation happening to mathematical quantities. Operators have many properties like linearity which often makes the analysis easy.
That being said, what operation does a Bellman operator do?. On what quantities does it operate?. What are the properties does it hold?. Before trying to answer all these, let’s see who is Bellman.
Some Historical Notes

Richard Ernest Bellman was an American applied mathematician. If you are from the tech industry chances are high that you probably heard about him before.
Perhaps the most popular thing from his inventory in today’s scenario is the ‘curse of dimensionality‘. It relates to the problem of an exponential increase in computational difficulty while adding extra dimensions to the mathematical space.
The driving technologies of today’s world are Artificial Intelligence (AI) and Machine Learning (ML). But we can say they were born realizing the challenges posed by the curse of dimensionality. AI and ML use approximate solution methods to tackle this problem.
He is also known for Dynamic Programming (DP) which again tries to tackle the exponential dimensionality problem. We can say that DP follows the idea of “don’t reinvent the wheel” and make use of intermediate results for computations.
Bellman Operator in Reinforcement Learning
Bellman’s ideas are best applied in problems of recursive nature. In RL we have the value function whose present value depends upon the value in the previous state. The value function assigns a numerical value for being in a state. The higher the value will be the better the state we are in.
In simple terms, my bank balance today will be depending upon my balance from the past. A student’s final grades will depend upon all the hard work she/he will put in many days before the final exam. The recursive nature of returns in RL and some visual intuitions are documented here.
In the form of an equation, the Bellman equation says the value of being in the current state will be the immediate reward plus the discounted version of all the future reward an agent is going to get. Lets us take a look at a simplified version of the Bellman equation.
$v(s) = \cal{R}_s+ \gamma\sum \cal{P}_{ss’} v(s’) $
Here $v$ represents the value function, $s$ current state, $s’$ next state, $R_s$ is the immediate reward, $\gamma$ is the discount factor, and $\cal{P}_{ss’}$ is the state transition probability.
This equation concisely tells that the value of being in the current state will be the immediate reward plus the discounted value of the next state value. Bellman equation holds this relation for all states.
The above equation ties up all such relations into a general equation using the properties of linear algebra. When expanded, the equation will look like the following.
\vdots \\ \cal{R}_n^\pi \end{bmatrix} +\gamma \begin{bmatrix} \cal{P}_{11}^\pi & \dots & \cal{P}_{1n}^\pi\\
\vdots & \ddots & \vdots\\ \cal{P}_{n1}^\pi & \dots & \cal{P}_{nn}^\pi \end{bmatrix} \begin{bmatrix}
v_\pi(1) \\ \vdots \\ v_\pi(n) \end{bmatrix} \right.$
Here the additional $\pi$ represents the policy an agent is following.
As you can see here, according to the equation, each state value is equated as a sum of respective immediate rewards plus discounted future values. This means the Bellman operator operates on the value function.
Mathematically this can be defined as an operator as shown below
$\cal{T^\pi}(v) = \cal{R}^\pi + \gamma \cal{P}^\pi v$
Hence Bellman operator maps state values to its next state values. The significance lies in the fact that Bellman operators have the property called contraction mapping. In simple terms, repeated application of the Bellman operator converges the value function to a fixed value.
Closing thoughts
We now have at least some first answers to the questions we had. As of now, today’s leading technologies rely heavily on approximation methods rather than analytical solutions. These concepts from Bellman have a different viewpoint on problem-solving by leveraging the recursive nature of problems. Who knows whether time will show us the rebirth of analytical methods!.
