The diverse properties of materials upon which material science researchers possess enormous enthusiasm are categorized into magnetic, transport, optical and superconducting properties. As we know, materials are made up of atoms comprised of electrons and nuclei and all these material properties originate from the interactions among electrons and atomic nuclei. Classical mechanics can describe the interaction among nuclei as it is massive compared to that of electron, keeping Hydrogen and Helium as exception. However, classical mechanics cannot govern the behavior of electrons and so it calls for quantum mechanics to describe the system. The electron structure theory in quantum mechanics describes the behavior of electron in materials. The distribution of electron in real space and in main energy levels is attributed to electron structure that determines cohesive energy of the material. The cohesive energy originated from electron structure in turn controls the structure of the material and thereby electronic structure plays a vital role in the aforementioned diverse material properties. Density Functional Theory (DFT) is a computational modeling method to achieve electronic structure calculations which is a precursor to novel material properties.
Why “density” and what is “functional” in DFT?
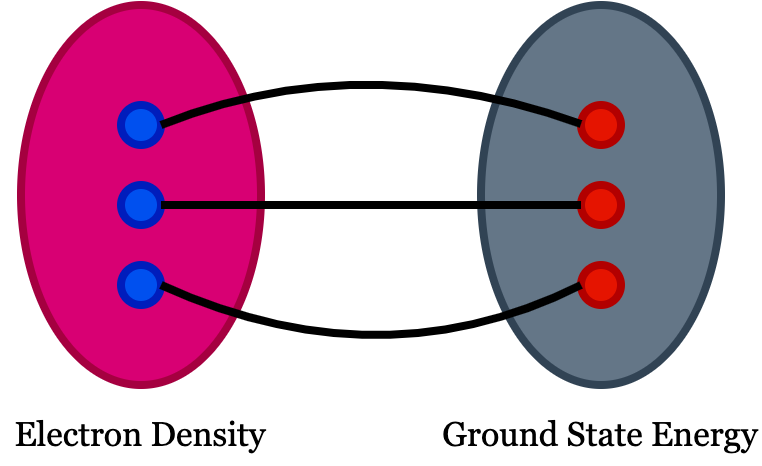
In DFT, the physical quantity of interest is electron density. You can see the definition of functional in google search as function of a function is functional! But in DFT, the meaning is slightly different, i.e., the functional in density functional theory means there exist one to one mapping between two fields which means there should be one to one correspondence between the function and the functional. If we have an easily solvable function and complex functional, solving the function will help you to understand the functional because of this one-to-one correspondence among them. In DFT, we use electron density as a functional to understand all ground-state properties of a material system.
Basic theorems (Hohenberg-Kohn theorems) in DFT
- The ground state energy extract from time independent Schrodinger equation is a unique function of the electron density.
- The electron density that minimizes the energy of overall functional is the true electron density corresponds to the complete solution of Schrodinger equation.
The Problem
A material’s ground state energy consists of n nuclei at positions $(x_1,x_2,..,x_n)$, which can be expressed as $E(x_1, x_2,..,x_n)$ and that defines the adiabatic potential energy surface representing the ground state energy. We need to understand how this energy changes when the atoms are set into motion. The electron density of any system determines the ground state energy of that system. In such a case, the total ground state energy of a many-electron system is a function of electron density. So, if we know the electron density functional, we can extract the system’s total energy.
Let’s have a look at the Schrodinger equation of a many electrons system,
| $[\dfrac{\hbar^2}{2m} \sum_{i=1}^{N}{\nabla_i}^2 + \sum_{i=1}^{N} V(r_i)+ \sum_{i=1}^{N} \sum_{j<i} U(r_i,r_j)] \psi =E \psi$ |
Where $\dfrac{\hbar^2}{2m} \sum_{i=1}^{N}{\nabla_i}^2$ is the Kinetic energy term, $\sum_{i=1}^{N} V(r_i)$ describes the interaction energy between each electron and the atomic nuclei, and $ \sum_{i=1}^{N} \sum_{j<i} U(r_i,r_j)$ represents the quantum mechanical interaction energy between different electrons .
In reality, we need to deal with n ($n$= 1 to$\infty$ ) dimensions in order to understand the interaction energy term of material systems with huge number of electrons. However, there are some points to make the problem a little simpler such as,
- If we know the ground state energy of the system, we can crack the problem as the Schrodinger equation is time-independent at the ground state and thereby overcome the mathematical complexity associated with time-dependent equations.
- We can approximate the wavefunction as the Hartree product which expresses the resultant wavefunction of a material system as a product of individual electron wavefunctions.
- The physical property of density in terms of the probability that ${\psi_i}^*(r)\psi_i(r)$ in our focus in DFT instead of electron position which helps to avoid the complexity of indistinguishability associated with the identical nature of electrons.
i.e. , $n(r) \approx \sum_{i=1} {\psi_i}^*(r)\psi_i(r)$
However, the complexity of DFT lies with accomplishing the one-to-one correspondence of this functional with easily solvable functions of a quantum mechanical system and the construction of this functional by selecting an appropriate set of wave functions. We can rewrite the total energy of this quantum mechanical system as,
$E(\psi_i)= E_{known}(\psi_i)+E_{X-C}(\psi_i)$
Here the known part of the energy consists of the kinetic energy of electrons, Coulomb interaction between the electron and nuclei, Coulomb interaction between pairs of nuclei, and the coulomb interaction between the pairs of electrons. The second part is called exchange-correlation functional representing all unknown quantum mechanical effects contributing to the total energy of the system. While doing DFT calculations, we have to choose the type of exchange-correlation functional based on the property of your interest. For instance, the local density approximation takes density as functional whereas the generalized gradient approximation (GGA) uses grad of electron density and meta GGA uses a second-order derivative of density and so on. We can decide on the suitable approximation among these by calculating the ground state energy given by each of these approximations. Whichever approximation gives minimum ground state energy, would be a more accurate approximation for your system. To perform DFT calculation, you have to use DFT packages and input atomic positions. The atomic positions can be extracted from molecule editing software such as Avagadro, VESTA, etc. So, identify a suitable package and go ahead to unravel the science encapsulated in electron density functional.
Pingback: Density Functional Theory Quantum