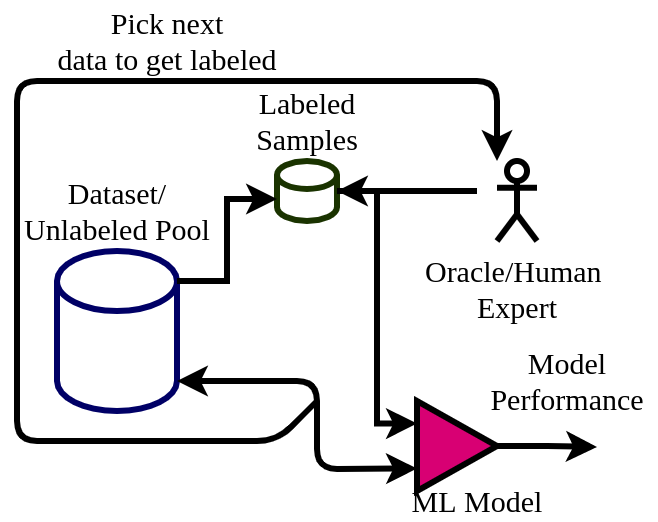This article is a reflection and articulation about the paper titled “Fair Active Learning” authored by Hadis Anahideh and Abolfazi Asudeh. The research paper is available on Arxiv and I am reviewing version 2 of it. The paper deal with bias in data and unfairness in the context of Active Learning.
Learning algorithms do their job in many domains, but the way they achieve is far from how humans learn. One of the easy examples of this is Adversarial Networks. A neural network trained to identify objects can be easily fooled by slight noise (not even visible for the human eyes) added to the image often resulting in wrong class prediction.
Other than the learning process is different for both humans and machines, supervised learning algorithms do see patterns that human learning ignores or unaware of. One such example is societal bias on gender.
Societal Bias and Proxy Attributes
Suppose you are recruiting candidates for a programmer role. As a knowledgeable person, you are aware that the gender of the person doesn’t matter when it comes to their programming competence level. But if you are giving the task to a learning algorithm, which depends on past historic data, it could be a problem.
Since the past, historic data of candidates may have fewer female programmers and they might have low scores as per the historic data which could be of reasons other than their competence level. It could be also possible to have any other features that indirectly represent gender creep into the data thereby creating the same problem.
The first problem is termed as inherent societal bias and the second problem is explained as proxy attributes in the paper.
Active Learning
Active Learning is a sub-discipline within semi-supervised machine learning where the learning algorithm interacts with an oracle (human expert) to get data labeled. A brief introduction to active learning and one of its algorithms employing uncertainty sampling is explained here.
A key component of active learning is the acquisition function which selects the datapoint to get labeled. This way the algorithm achieves its best possible performance with minimum datapoints.
The research paper proposes active learning algorithms which account for fairness quality in addition to entropy as a solution to this problem. The acquisition function here picks a datapoint to improve model performance as well as fairness. They have shown its efficacy with experiments on real-world data.
The Uncertainty Sampling Technique
We have seen in an earlier post how active learning uses entropy value to pick the most informative samples to get labeled. There the acquisition function was formalised in mathematical terms as follows.
$X* = \underset{\forall x \in U}{\mathrm{argmax}}\; – \sum_{k=1}^{K} P(y=k|X)logP(y=k|X)$
Here the argmax function is looking for a data point that maximizes the entropy as defined in the equation. But in this paper, the acquisition function is modified so that a simplex weightage is given to the entropy as well as a fairness measure. This was explained with an equation similar to below.
$\underset{\forall x \in U}{max}\; \alpha H+(1-\alpha)(1-F(C))$
Here $H$ is the entropy term and the second term corresponds to the fairness quantity.
The key idea here is, by smartly selecting samples to label, the potential of active learning to mitigate algorithmic bias is leveraged.
In the earlier post, we have seen the intuition behind how entropy represents the uncertainty of a model’s prediction about the class of a data point. But how does the fairness measure is handled programmatically or algorithmically?. This is done by considering demographic Parity.
Demographic Parity
For a classifier having demographic parity, all groups within a data set will have the same acceptance rate. In the recruitment scenario discussed before, with demographic parity suppose if $\rho$ is the ratio of females in the applicant pool, Ideally the same fraction of females should be selected as per the classifier.
The authors give a couple of ways this can be formulated mathematically including mutual information and covariance. This means under demographic parity the mutual information between the variables gender information and getting selected will be zero.
With these two selection criteria, the simplex weighted equation is used to construct the proposed Fair Active Learning algorithm.
The authors have evaluated the performance of the proposed algorithm on the COMPAS dataset which contains information such as marital status, race, age, etc. The performance metrics used were including accuracy, fairness measure, F1-score, precision, and recall. The proposed fair active learning algorithm showed a fairness improvement of about 50% compared to standard active learning models.
Concluding Thoughts
This paper takes an interesting approach by using active learning to fight algorithmic bias. Upcoming years of AI and ML will be judged on their ability/inability to handle bias and ethics. Particularly the mathematical formulation of fairness measures is interesting while being simple. One potential future step seems to come up with some creative ways to deal with the accuracy and fairness tradeoff.